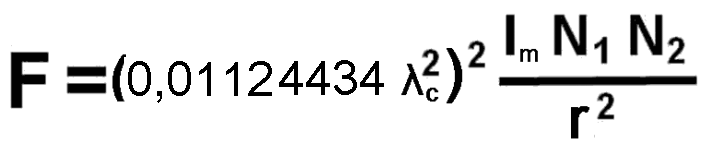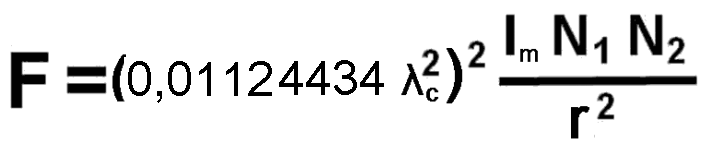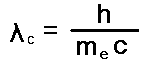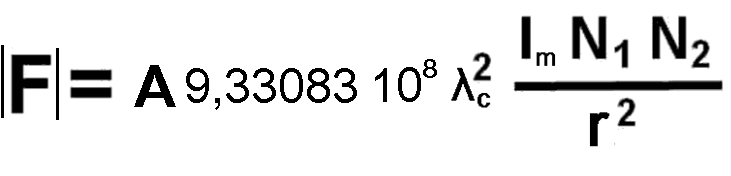Electromagnetic nature of gravity.

The following formula does not include masses or charges (it only includes the number N of nucleons, such as neutrons and protons in atomic nuclei) and therefore it has very good conditions for an integration of gravitation with the other types of interaction, like electromagnetic interaction or nuclear forces. This formula # 1 applies to gravity everywhere. This is a new formula for thinking about the four fundamental interactions (the four basic forces of physics) in the universe. This formula allows gravity to be calculated, but at the same time it allows the reality of gravity to be better recognized, if this representation were closer to the reality of sword power. I explained how it came about with a simple theory below.

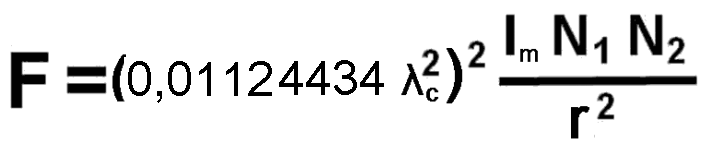
Formula No. 1.

The variables are only explained below for gravity. The Compton wavelength of an electron λ_c can be calculated using the following formula:

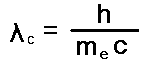
The number of all nucleons N in a body is calculated using the following simple formula:
N = m / u
m - the mass of a body
u - the atomic mass unit
F - Gravity in [N] (Newtons)
r - Distance between the centers of bodies in [m]
I_m - Energy density of electromagnetic radiation from black bodies at a temperature of 2.725° K in [ J / m³ ]
I_m = 4,2 10 ^-14 [J / m³])
N₁ - the total number of nucleons in the first body
N₂ -the total number of nucleons in the second body
I used the following formulas to calculate energy density I:
I = (P/A) 4/c
P/A = a T⁴
wo:
P - Radiant power of a body
A - Area in which the radiation is emitted
c - Speed of light in a vacuum
a - is Steffen-Bolzmann constant .
a = 5,67 10^-8 W/(m²K⁴)
Here e means the value of elementary charge. This equation can also be reduced and this gives a new formula 7 for coulob force, as below with an adjustment factor A equal to 1 m²:

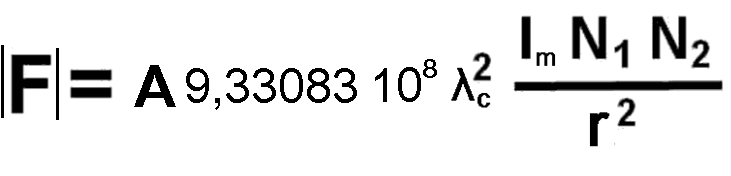
Formula 7

So you can represent the two interactions and a single radiation in a similar way as finding the cause of the two forces. That would be microwave radiation, the temperature of which almost corresponds to the temperature of background radiation.
Are the two formulas a representation of reality or just a coincidence?
I would venture an experiment as to whether the energy density of microwave radiation actually affects electrical power between two charged bodies.